Entropy is one of those words that shows up across physics, chemistry, information theory, biology and cosmology — and it means slightly different things in each context. At its heart entropy quantifies how many ways a system can be arranged (statistical view), how uncertain we are about a system (information view), and why natural processes have a preferred direction (thermodynamic arrow of time).
This blog walks through entropy rigorously: definitions, core equations, experimental checks, paradoxes (Maxwell’s demon), modern extensions (information and quantum entropy), and applications from engines to black holes.
What you’ll get here
- Thermodynamic definition and Clausius’ relation
- Statistical mechanics (Boltzmann & Gibbs) and microstates vs macrostates
- Shannon (information) entropy and its relation to thermodynamic entropy
- Key equations and worked examples (including numeric Landauer bound)
- Second law, Carnot efficiency, and irreversibility
- Maxwell’s demon, Szilard engine and Landauer’s resolution
- Quantum (von Neumann) entropy and black-hole entropy (Bekenstein–Hawking)
- Non-equilibrium entropy production, fluctuation theorems and Jarzynski equality
- Entropy in chemistry, biology and cosmology
- Practical measuring methods, common misconceptions and further reading
Thermodynamic entropy — Clausius and the Second Law
Historically entropy ![]() entered thermodynamics via Rudolph Clausius (1850s). For a reversible process the change in entropy is defined by the heat exchanged reversibly divided by temperature:
entered thermodynamics via Rudolph Clausius (1850s). For a reversible process the change in entropy is defined by the heat exchanged reversibly divided by temperature:
![]()
For a cyclic reversible process the integral is zero; for irreversible processes Clausius’ inequality gives:
![]()
with equality for reversible changes. The Second Law is commonly stated as:
For an isolated system, the entropy never decreases:
.
Units: entropy is measured in joules per kelvin (J·K⁻¹).
Entropy and spontaneity: For processes at constant temperature and pressure, the Gibbs free energy tells us about spontaneity:
![]()
A process is spontaneous if ![]() .
.
Statistical mechanics: Boltzmann’s insight
Thermodynamic entropy becomes precise in statistical mechanics. For a system with ![]() microstates compatible with a given macrostate, Boltzmann gave the famous formula:
microstates compatible with a given macrostate, Boltzmann gave the famous formula:
![]() ,
,
where ![]() is Boltzmann’s constant (
is Boltzmann’s constant (![]() ).
).
Microstates vs macrostates:
- Microstate — complete specification of the microscopic degrees of freedom (positions & momenta).
- Macrostate — macroscopic variables (energy, volume, particle number). Many microstates can correspond to one macrostate; the multiplicity is
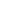 .
.
This is the bridge: large ![]() → large
→ large ![]() . Entropy counts microscopic possibilities.
. Entropy counts microscopic possibilities.
Gibbs entropy and canonical ensembles
For a probability distribution over microstates ![]() , Gibbs generalized Boltzmann’s formula:
, Gibbs generalized Boltzmann’s formula:
![]()
For the canonical (constant ![]() ) ensemble:
) ensemble: ![]() and partition function
and partition function ![]() , one obtains thermodynamic relations like:
, one obtains thermodynamic relations like:
![]() .
.
Gibbs’ form makes entropy a property of our probability assignment over microstates — perfect for systems in thermal contact or with uncertainty.
Information (Shannon) entropy and its link to thermodynamics
Claude Shannon defined an entropy for information:
![]()
The connection to thermodynamic entropy is direct:
![]()
So one bit of uncertainty corresponds to an entropy of ![]() J·K⁻¹.This equivalence underlies deep results connecting information processing to thermodynamics (see Landauer’s principle below).
J·K⁻¹.This equivalence underlies deep results connecting information processing to thermodynamics (see Landauer’s principle below).
The Second Law, irreversibility and the arrow of time
- Statistical: Lower-entropy macrostates (small
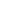 ) are vastly less probable than higher-entropy ones.
) are vastly less probable than higher-entropy ones. - Dynamical/thermodynamic: Interactions with many degrees of freedom transform organized energy (work) into heat, whose dispersal increases entropy.
Entropy increase defines the thermodynamic arrow of time: microscopic laws are time-symmetric, but initial low-entropy conditions (early universe) plus statistical behavior produce a preferred time direction.
Carnot engine and entropy balance — efficiency limit
Carnot’s analysis links entropy to the maximum efficiency of a heat engine operating between a hot reservoir at ![]() and cold reservoir at
and cold reservoir at ![]() .For a reversible cycle:
.For a reversible cycle:
![]()
This is derived from entropy conservation for the reversible cycle: net entropy change of reservoirs is zero, so energy flows are constrained and efficiency is bounded.
Maxwell’s demon, Szilard engine, and Landauer’s principle
Maxwell’s demon (1867) is a thought experiment in which a tiny “demon” can, by sorting molecules, apparently reduce entropy and violate the Second Law. Resolution comes from information theory: measurement and memory reset have thermodynamic costs.
Szilard engine (1929): by measuring which side the molecule is on, one can extract at most ![]() work.The catch: resetting the demon’s memory (erasure) costs at least
work.The catch: resetting the demon’s memory (erasure) costs at least ![]() energy — that restores the Second Law.
energy — that restores the Second Law.
Landauer’s Principle (1961)
Landauer’s principle formalizes the thermodynamic cost of erasing one bit:
![]()
Worked numeric example (Landauer bound at room temperature):
- Boltzmann constant:
 .
. - Room temperature (typical):
 .
. - Natural logarithm of 2:
 .
.
Stepwise calculation
- Multiply Boltzmann constant by temperature:
![]()
- Multiply by
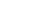 :
:
![]()
So, erasing one bit at ![]() requires at least:
requires at least:![]() Conversion to electronvolts (eV):1 eV =
Conversion to electronvolts (eV):1 eV = ![]()
![]()
This tiny energy is relevant when pushing computation to thermodynamic limits (ultra-low-power computing, reversible computing, quantum information).
Quantum entropy — von Neumann entropy
For quantum systems represented by a density matrix ![]() , the von Neumann entropy generalizes Gibbs:
, the von Neumann entropy generalizes Gibbs:
![]()
- For a pure state ∣ψ⟩⟨ψ∣, ρ^2=ρ and:
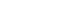
- For mixed states (statistical mixtures),
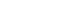
Von Neumann entropy is crucial in quantum information (entanglement entropy, channel capacities, quantum thermodynamics).
Entropy in cosmology and black-hole thermodynamics
Two striking applications:
Cosmology: The early universe had very low entropy (despite high temperature) because gravity-dominated degrees of freedom were in a highly ordered state (smoothness). The growth of structure (galaxies, stars) and local decreases of entropy are consistent with an overall rise in total entropy.
Black hole entropy (Bekenstein–Hawking): Black holes have enormous entropy proportional to their horizon area ![]() :
:
![]()
This formula suggests entropy scales with area, not volume — a deep hint at holography and quantum gravity. Associated with that is Hawking radiation and a black hole temperature ![]() , giving black holes thermodynamic behavior and posing the information-paradox puzzles that drive modern research.
, giving black holes thermodynamic behavior and posing the information-paradox puzzles that drive modern research.
Non-equilibrium entropy production and fluctuation theorems
Classical thermodynamics mainly treats equilibrium or near-equilibrium. Modern advances study small systems and finite-time processes:
- Entropy production rate:
 quantifies irreversibility.
quantifies irreversibility. - Fluctuation theorems (Evans–Searles, Crooks) quantify the probability of transient violations of the Second Law in small systems (short times): they say that entropy can decrease for short times, but the likelihood decays exponentially with the magnitude of the violation.
- Jarzynski equality links non-equilibrium work
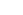 to equilibrium free-energy differences ΔF:
to equilibrium free-energy differences ΔF:
![]() ,
,
where ![]() and ⟨⋅⟩ denotes average over realizations. The Jarzynski equality has been experimentally verified in molecular pulling experiments (optical tweezers etc.) and is a powerful tool in small-system thermodynamics.
and ⟨⋅⟩ denotes average over realizations. The Jarzynski equality has been experimentally verified in molecular pulling experiments (optical tweezers etc.) and is a powerful tool in small-system thermodynamics.
Entropy in chemistry and biology
Chemistry: Entropy changes determine reaction spontaneity viay: ![]() . Phase transitions (melting, boiling) involve characteristic entropy changes (latent heat divided by transition temperature).
. Phase transitions (melting, boiling) involve characteristic entropy changes (latent heat divided by transition temperature).
Biology: Living organisms maintain local low entropy by consuming free energy (food, sunlight) and exporting entropy to their environment. Schrödinger’s What is Life? introduced the idea of “negative entropy” (negentropy) as essential for life. In biochemical cycles, entropy production links to metabolic efficiency and thermodynamic constraints on molecular machines.
Measuring entropy
Direct measurement of entropy is uncommon — we usually measure heat capacities or heats of reaction and integrate:
![]() .
.
Calorimetry gives ![]() and latent heats; statistical estimations use measured distributions
and latent heats; statistical estimations use measured distributions ![]() to compute:
to compute:![]() . In small systems, one measures trajectories and verifies fluctuation theorems or Jarzynski equality.
. In small systems, one measures trajectories and verifies fluctuation theorems or Jarzynski equality.
Common misconceptions (clarified)
- Entropy = disorder?
That phrase is a useful intuition but can be misleading. “Disorder” is vague. Precise: entropy measures the logarithm of multiplicity (how many microstates correspond to a macrostate) or uncertainty in state specification. - Entropy always increases locally?
No — local decreases are possible (ice forming, life evolving) as long as the total entropy (system + environment) increases. Earth is not isolated; it receives low-entropy energy (sunlight) and exports higher-entropy heat. - Entropy and complexity:
High entropy does not necessarily mean high complexity (random noise has high entropy but low structure). Complex ordered structures can coexist with high total entropy when entropy elsewhere increases.
Conceptual diagrams (text descriptions you can draw)
- Microstates/Macrostates box: Draw a box divided into many tiny squares (microstates). Highlight groups of squares that correspond to two macrostates: Macrostate A (few squares) and Macrostate B (many squares). Label
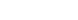 . Entropy
. Entropy  .
. - Heat engine schematic: Hot reservoir
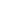 → engine → cold reservoir
→ engine → cold reservoir 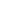 . Arrows show
. Arrows show 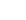 into engine,
into engine, 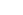 out,
out,  rejected; annotate entropy transfers
rejected; annotate entropy transfers 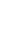 and
and  .
. - Szilard box (single molecule): A box with a partition and a molecule that can be on left or right; show measurement, work extraction
 , and memory erasure cost
, and memory erasure cost  .
. - Black hole area law: Draw a sphere labeled horizon area
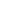 and annotate
and annotate .
.
Applications & modern implications
- Cosmology & quantum gravity: Entropy considerations drive ideas about holography, information loss, and initial conditions of the universe.
- Computer science & thermodynamics: Landauer’s bound places fundamental limits on energy per logical operation; reversible computing aims to approach zero dissipation by avoiding logical erasure.
- Nano-devices and molecular machines: Entropy production sets limits on efficiency and speed.
- Quantum information: Entanglement entropy and thermalization in isolated quantum systems are active research frontiers.
Further reading (selective)
Introductory
- Thermal Physics by Charles Kittel and Herbert Kroemer — accessible intro to thermodynamics & statistical mechanics.
- An Introduction to Thermal Physics by Daniel V. Schroeder — student friendly.
Deeper / Technical
- Statistical Mechanics by R.K. Pathria & Paul Beale.
- Statistical Mechanics by Kerson Huang.
- Lectures on Phase Transitions and the Renormalization Group by Nigel Goldenfeld (for entropy in critical phenomena).
Information & Computation
- R. Landauer — “Irreversibility and Heat Generation in the Computing Process” (1961).
- C. E. Shannon — “A Mathematical Theory of Communication” (1948).
- Cover & Thomas — Elements of Information Theory.
Quantum & Gravity
- Sean Carroll — popular and technical writings on entropy and cosmology.
- J. D. Bekenstein & S. W. Hawking original papers on black hole thermodynamics.
Final Thoughts
Entropy is a unifying concept that appears whenever we talk about heat, uncertainty, information, irreversibility and the direction of time. Its mathematical forms —
![]() ,
,![]() ,
,
![]()
— all capture the same core idea: the count of possibilities or the degree of uncertainty. From heat engines and chemical reactions to the limits of computation and the thermodynamics of black holes, entropy constrains what is possible and helps us quantify how nature evolves.
Leave a Reply