Markov chains are one of the most widely useful mathematical models for random systems that evolve step-by-step with no memory except the present state. They appear in probability theory, statistics, physics, computer science, genetics, finance, queueing theory, machine learning (HMMs, MCMC), and many other fields. This guide covers theory, equations, classifications, convergence, algorithms, worked examples, continuous-time variants, applications, and pointers for further study.
What is a Markov chain?
A (discrete-time) Markov chain is a stochastic process ![]() on a state space
on a state space ![]() (finite or countable, sometimes continuous) that satisfies the Markov property:
(finite or countable, sometimes continuous) that satisfies the Markov property:
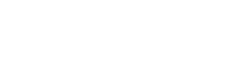
The future depends only on the present, not the full past.
We usually describe a Markov chain by its one-step transition probabilities. For discrete state space ![]() define the transition matrix
define the transition matrix ![]() with entries
with entries
![]() .
.
By construction, every row of ![]() sums to 1:
sums to 1:
![]() for all
for all ![]() .
.
If ![]() is finite with size
is finite with size ![]() is an
is an ![]() row-stochastic matrix.
row-stochastic matrix.
Multi-step transitions and Chapman–Kolmogorov
The ![]() -step transition probabilities are entries of the matrix power
-step transition probabilities are entries of the matrix power ![]() :
:
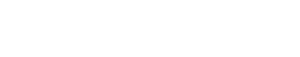
They obey the Chapman–Kolmogorov equations: ![]() ,
,
or in entries
![]() .
.
The ![]() -step probabilities are just matrix powers:
-step probabilities are just matrix powers: ![]() .
.
Examples (simple and illuminating)
1. Two-state chain (worked example)
State space ![]() . Let
. Let  .
.
Stationary distribution ![]() satisfies
satisfies ![]() and
and ![]() . Write
. Write ![]() .
.
From ![]() we get (component equations)
we get (component equations)
![]() .
.
Rearrange: ![]() so
so ![]() . Divide both sides by
. Divide both sides by ![]() (digit-by-digit):
(digit-by-digit): ![]() , therefore
, therefore
![]() .
.
Using normalization ![]() gives
gives ![]() so
so ![]() . Then
. Then ![]() .
.
So the stationary distribution is ![]() .
.
(You can check: ![]() e.g. first component
e.g. first component ![]()
2. Simple random walk on a finite cycle
On states ![]() with
with ![]() and
and ![]() . If
. If ![]() the stationary distribution is uniform:
the stationary distribution is uniform: ![]() .
.
Classification of states
For a Markov chain on countable ![]() , states are classified by accessibility and recurrence.
, states are classified by accessibility and recurrence.
- Accessible:
 if
if 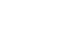 for some
for some 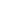 .
. - Communicate:
 if both
if both  and
and  . Communication partitions
. Communication partitions  into classes.
into classes.
For a state ![]() :
:
- Transient: with probability < 1 you ever return to
 .
. - Recurrent (persistent): with probability 1 you eventually return to
 .
.- Positive recurrent: expected return time
![Rendered by QuickLaTeX.com \mathbb{E} [\tau_i]<$\infty$](https://elasticstrain.com/wp-content/ql-cache/quicklatex.com-0993cc7d96152089fcb7c00344d42c2a_l3.png) .
. - Null recurrent: expected return time infinite.
- Positive recurrent: expected return time
- Periodic: the period
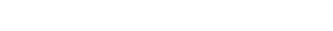 .If
.If 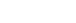 the state is aperiodic.
the state is aperiodic.
Important facts:
- Communication classes are either all transient or all recurrent.
- In a finite state irreducible chain, all states are positive recurrent; there exists a unique stationary distribution.
Stationary distributions and invariant measures
A probability vector ![]() (row vector) is stationary if
(row vector) is stationary if ![]() .
.
If the chain starts in ![]() then it is stationary (the marginal distribution at every time is
then it is stationary (the marginal distribution at every time is ![]() ).
).
For irreducible, positive recurrent chains, a unique stationary distribution exists. For finite irreducible chains it is guaranteed.
Detailed balance and reversibility
A stronger condition is detailed balance: ![]() for all
for all ![]() .
.
If detailed balance holds, the chain is reversible (time-reversal has the same law). Many constructions (e.g., Metropolis–Hastings) enforce detailed balance to guarantee ![]() is stationary.
is stationary.
Convergence, ergodicity, and mixing
Ergodicity
An irreducible, aperiodic, positive recurrent Markov chain is ergodic: for any initial distribution ![]() ,
,
![]() ,
,
i.e., the chain converges to the stationary distribution.
Total variation distance
Define total variation distance between two distributions μ,ν on S: ![]() .
.
The mixing time ![]() is the smallest
is the smallest ![]() such that
such that ![]() .
.
Spectral gap and relaxation time (finite-state reversible chains)
For a reversible finite chain, the transition matrix ![]() has real eigenvalues
has real eigenvalues ![]() . Roughly,
. Roughly,
- The time to approach stationarity scales like
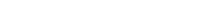 .
. - Larger spectral gap → faster mixing.
(There are precise inequalities; the spectral approach is fundamental.)
Hitting times, commute times, and potential theory
Let ![]() time to hit set
time to hit set ![]() be the hitting time of set
be the hitting time of set ![]() . For expected hitting times
. For expected hitting times ![]() you can solve linear equations:
you can solve linear equations:  .
.
These linear systems are effective in computing mean times to absorption, cover times, etc. In reversible chains there are intimate connections between hitting times, electrical networks, and effective resistance.
Continuous-time Markov chains (CTMC)
Discrete-time Markov chains jump at integer times. In continuous time we have a Markov process with generator matrix ![]() satisfying, for
satisfying, for ![]() ,
, ![]() , and
, and
For a CTMC the transition function ![]()
and Kolmogorov forward/backward equations hold:
- Forward (Kolmogorov):
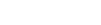 .
. - Backward:
 .
.
Poisson process and birth–death processes are prototypical CTMCs. For birth–death with birth rates ![]() and death rates
and death rates ![]() , the stationary distribution (if it exists) has product form:
, the stationary distribution (if it exists) has product form:
![]() .
.
Examples of important chains
- Random walk on graphs:
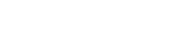 edge. Stationary
edge. Stationary 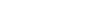 .
. - Birth–death chains: 1D nearest-neighbour transitions with closed-form stationary formulas.
- Glauber dynamics (Ising model): Markov chain on spin configurations used in statistical physics and MCMC.
- PageRank: random surfer with teleportation; stationary vector solves
 for Google matrix
for Google matrix  .
. - Markov chain Monte Carlo (MCMC): design
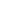 with target stationary
with target stationary 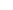 (Metropolis–Hastings, Gibbs).
(Metropolis–Hastings, Gibbs).
Markov Chain Monte Carlo (MCMC)
Goal: sample from a complicated target distribution ![]() on large state space. Strategy: construct an ergodic chain with stationary distribution
on large state space. Strategy: construct an ergodic chain with stationary distribution ![]() .
.
Metropolis–Hastings
Given proposal kernel ![]() :
:
Acceptance probability ![]() .
.
Algorithm:
- At state
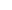 , propose
, propose 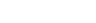 .
. - With probability
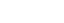 move to
move to 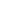 ; otherwise stay at
; otherwise stay at 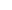 .
.
This enforces detailed balance and hence stationarity.
Gibbs sampling
A special case where the proposal is the conditional distribution of one coordinate given others; always accepted.
MCMC performance is measured by mixing time and autocorrelation; diagnostics include effective sample size, trace plots, and Gelman–Rubin statistics.
Limits & limit theorems
- Ergodic theorem for Markov chains: For ergodic chain and function
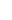 with
with ![Rendered by QuickLaTeX.com {\mathbb{E}_\pi[|f|] < \infty}](https://elasticstrain.com/wp-content/ql-cache/quicklatex.com-72fa532587c974f9c3b79ce3660165a1_l3.png) ,
,
![]() ,
,
i.e. time averages converge to ensemble averages.
- Central limit theorem (CLT): Under mixing conditions,
![Rendered by QuickLaTeX.com \sqrt{n} (\overline{f_n} - \mathbb{E}_{\pi}[f])](https://elasticstrain.com/wp-content/ql-cache/quicklatex.com-6062cce9a064b8988528948ede27f6a0_l3.png) converges in distribution to a normal with asymptotic variance expressible via the Green–Kubo formula (autocovariance sum).
converges in distribution to a normal with asymptotic variance expressible via the Green–Kubo formula (autocovariance sum).
Tools for bounding mixing times
- Coupling: Construct two copies of the chain started from different initial states; if they couple (meet) quickly, that yields bounds on mixing.
- Conductance (Cheeger-type inequality): Define for distribution
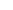 ,
,
![]() .
.
A small conductance implies slow mixing. Cheeger inequalities relate ![]() to the spectral gap.
to the spectral gap.
- Canonical paths / comparison methods for complex chains.
Hidden Markov Models (HMMs)
An HMM combines a Markov chain on hidden states with an observation model. Important algorithms:
- Forward algorithm: computes likelihood efficiently.
- Viterbi algorithm: finds most probable hidden state path.
- Baum–Welch (EM): learns HMM parameters from observed sequences.
HMMs are used in speech recognition, bioinformatics (gene prediction), and time-series modeling.
Practical computations & linear algebraic viewpoint
- Stationary distribution ππ solves linear system
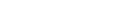 with normalization
with normalization 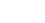 =1.
=1. - For large sparse
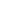 , compute
, compute 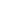 by power iteration: repeatedly multiply an initial vector by
by power iteration: repeatedly multiply an initial vector by 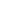 until convergence (this is the approach used by PageRank with damping).
until convergence (this is the approach used by PageRank with damping). - For reversible chains, solving weighted eigen problems is numerically better.
Common pitfalls & intuition checks
- Not every stochastic matrix converges to a unique stationary distribution. Need irreducibility and aperiodicity (or consider periodic limiting behavior).
- Infinite state spaces can be subtle: e.g., simple symmetric random walk on
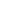 is recurrent in 1D and 2D (returns w.p. 1) but null recurrent in 1D/2D (no finite stationary distribution); in 3D it’s transient.
is recurrent in 1D and 2D (returns w.p. 1) but null recurrent in 1D/2D (no finite stationary distribution); in 3D it’s transient. - Ergodicity vs. speed: Existence of
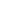 does not imply rapid mixing; chains can be ergodic but mix extremely slowly (metastability).
does not imply rapid mixing; chains can be ergodic but mix extremely slowly (metastability).
Applications (selective)
- Search & ranking: PageRank.
- Statistical physics: Monte Carlo sampling, Glauber dynamics, Ising/Potts models.
- Machine learning: MCMC for Bayesian inference, HMMs.
- Genetics & population models: Wright–Fisher and Moran models (Markov chains on counts).
- Queueing theory: Birth–death processes, M/M/1 queues modeled by CTMCs.
- Finance: Regime-switching models, credit rating transitions.
- Robotics & control: Markov decision processes (MDPs) extend Markov chains with rewards and control.
Conceptual diagrams (you can draw these)
- State graph: nodes = states; directed edges
 labeled by
labeled by 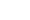 .
. - Transition matrix heatmap: show
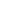 colors; power-iteration evolution of a distribution vector.
colors; power-iteration evolution of a distribution vector. - Mixing illustration: plot total-variation distance
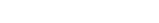 vs
vs 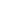 .
. - Coupling picture: two walkers from different starts that merge then move together.
Further reading and resources
- Introductory
- J. R. Norris, Markov Chains — clear, readable.
- Levin, Peres & Wilmer, Markov Chains and Mixing Times — excellent for mixing time theory and applications.
- Applied / Algorithms
- Brooks et al., Handbook of Markov Chain Monte Carlo — practical MCMC methods.
- Rabiner, A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition.
- Advanced / Theory
- Aldous & Fill, Reversible Markov Chains and Random Walks on Graphs (available online).
- Meyn & Tweedie, Markov Chains and Stochastic Stability — ergodicity for general state spaces.
Quick reference of key formulas (summary)
- Chapman–Kolmogorov:
 .
. - Stationary distribution:
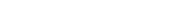 .
. - Detailed balance (reversible):
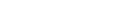 .
. - Expected hitting time system:
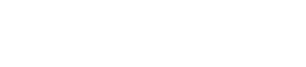
- CTMC generator relation:
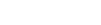 ,
,  .
.
Final thoughts
Markov chains are deceptively simple to define yet enormously rich. The central tension is between local simplicity (memoryless one-step dynamics) and global complexity (long-term behavior, hitting times, mixing). Whether you need to analyze a queue, design a sampler, or reason about random walks on networks, Markov chain theory supplies powerful tools — algebraic (eigenvalues), probabilistic (hitting/return times), and algorithmic (coupling, MCMC).
Leave a Reply